Quaternions part 2

In the previous post, we introduced quaternions and discussed some of their basic properties. Quaternions are often used in 3D applications such as graphics and robotics to perform smooth rotations.

In this post we describe how to use quaternions to represent points in 3D and how to use quaternion operations to perform rotations about an arbitrary axis.

Suppose we have a point $P$ with coordinates $(p_x, p_y, p_z)$. We would like to rotate $P$ about the axis $u=(u_x,u_y, u_z)$ by an angle of $\theta$. Let us denote the rotated point by $P'$.

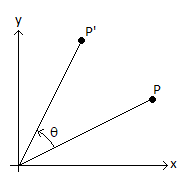
To calculate the coordinates of $P'$, we first represent the point $P$ with the following quaternion:

$p = p_xi + p_yj + p_zk.$

We then use the rotation axis and angle to form the following unit quaternion:
$q = cos(\theta/2) + sin(\theta/2)(u_xi + u_yj + u_zk).$
Finally, we calculate $p'$ by forming the product:
$p' = qpq^*,$
where $q^*$ is the conjugate of $q$ (see the previous post for details). On inspecting the components of $p'$, we should find that the real part is zero. The three complex components $p'_x, p'_y, p'_z$ give us the coordinates for $P'$.